Faasitasakaal

Faasimuutused mõjutavad protsesse. Neid kasutatakse separatsiooni protsessides, et puhastada kemikaale ja muid toote. On oluline siis arvutada tingimusi, kus kaks faasi tekivad.

Faasitasakaalu tingimused

Faasitasakaal esineb siis, kui mõlema faasi keemilised potentsiaalid on võrdsed kõikide ainete jaoks. Kuna keemiline potentsiaal ei käitu ilusti matemaatiliselt, saab samuti leida faasitasakaalu fugitiivsustega.

\[ μ_{i,faas\ 1} = μ_{i,faas\ 2} \]

\[ f_{i,faas\ 1} = f_{i,faas\ 2} \]

Ideaalne tasakaal

Kuidas me saame fugitiivsust arvutada? Alustame kõige lihtsama olukorraga, ehk kui on ideaalgaas tasakaalus ideaalse seguga. Ideaalgaasi jaoks fugitiivsus on lihtsalt aine osarõhk.

\[ f_{i,gaas} = P_i = y_i P \]

y_i on aine moolosa gaasifaasis.

Peame arvutama ka aine vedelfaasi fugitiivsust. Puhta aine jaoks vedeliku fugitiivsus võrdub süsteemi rõhuga, mis on lihtsalt aine aururõhk (P^sat).

\[ f_{i,vedel} = P = P^{sat} \]

Ja ideaalses süsteemis võime eeldata, et aine vedelfaasi fugitiivsus on lihtsalt aururõhk korrutatud vedelfaasi moolosaga. Kuna faasitasakaalus aine fugitiivsused mõlemas faasis peab olema võrdsed, siis saame lõpuks sellise valemi faasitasakaalu jaoks.

\[ y_i P = x_i P^{sat} \]

Seda valemit kutsutakse Raoulti seaduseks.

Reaalsed segud

Loomulikult, reaalses elus molekulide vahelised tõmbejõud on olulised ja Raoulti seadus tihti ei vasta reaalsele olukorrale. Vaata näiteks, kuidas 3-metüülpentaani ja 2-metüül-2-propanooli segu erineb Raoulti seadusest.

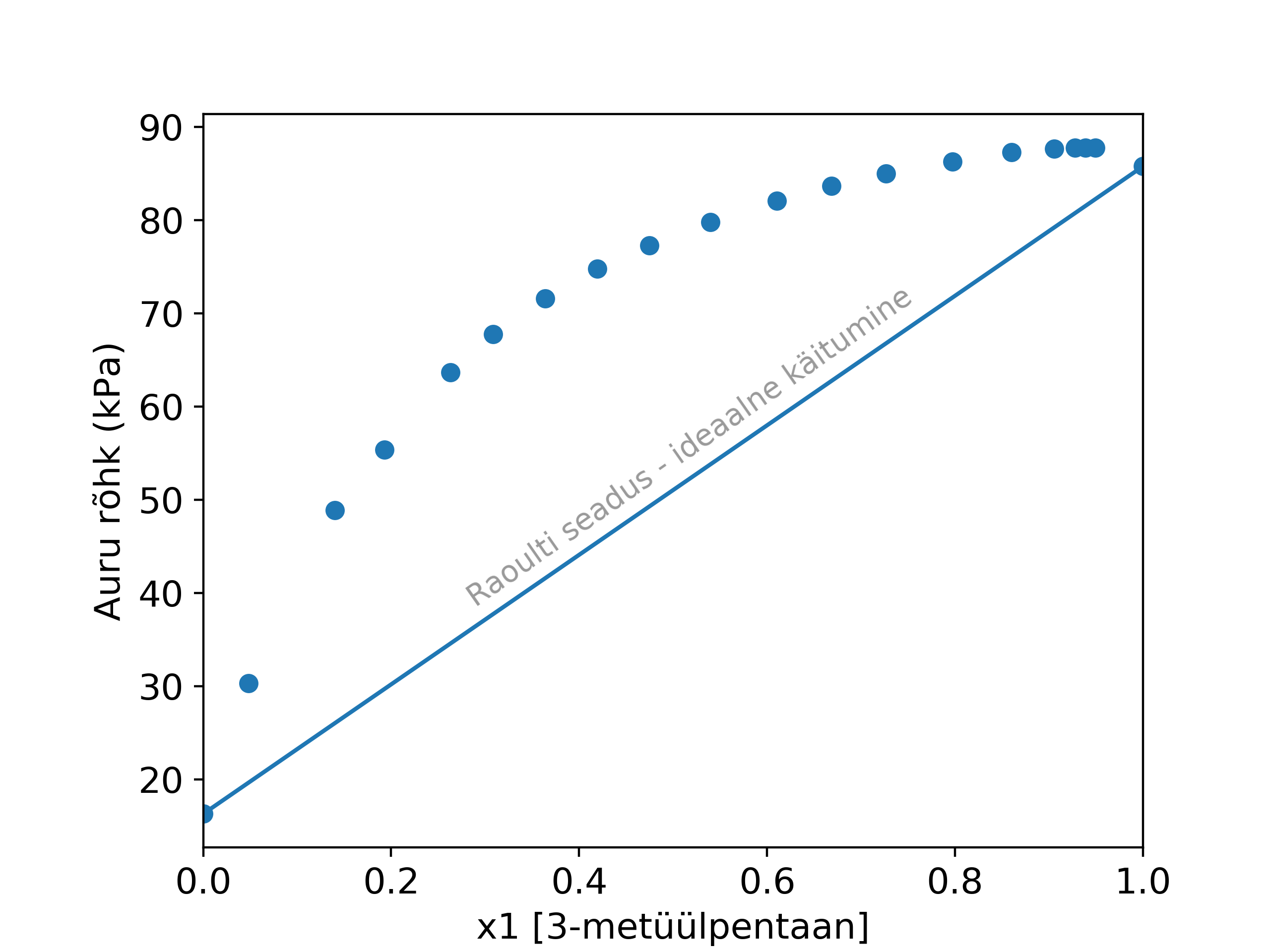
3-metüülpentaani + 2-metüül-2-propanooli segu auru rõhk temperatuuril 331,5 K¹

Selleks, et hinnata süsteemi erinevust ideaalolekust, kasutatakse tihti jääkomadusi. Jääkomadus (ingl residual property) arvutatakse lahutades ideaalväärtust aine/segu tegeliku omaduse väärtusest. Jääkomadustega on võimalik paremini näha, kuidas molekulide vahelised jõud mõjutavad segu omadust.

\[ Θ^{res} = Θ - Θ^{ig} \]

Faasitasakaalu arvutustes kasutatakse tavaliselt fugitiivsuse koefitsienti (φ), mis on sisuliselt jääkomadus.

\[ μ_{i}^{res} = μ_i - μ_i^{ig} = RT \ln φ_i \]

Fugitiivsuse koefitsient näitab erinevust referentsolekust. Tavaliselt referentsina kasutatakse ideaalgaasi olekut, ehk olek, milles fugitiivsus võrdub aine osarõhuga.

\[ φ_i = \frac{f_i}{f_i^{ig}} = \frac{f_i}{x_i P} \]

Mõnikord kasutatakse ka lõpmatu lahjenduse olekut. Seda kasutatakse näiteks soolalahuste jaoks kuna puhas sool on hoopis tahke. Aine oma osarõhu asemel kasutatakse hoopis lahusti puhta aine fugitiivsust referentsina.

Reaalse segu tasakaal

Kuna fugitiivsuse koefitsient näitab kõrvalekallet ideaalsest olukorrast, saame seda lisada Raoulti seadusele, et modelleerida faasitasakaalu reaalsete ainete jaoks. Seda meetodit kutsutakse mõnikord φ-φ meetodiks.

\[ f_i = x_i φ_i P \]

\[ y_i φ_{i,gaas} P = x_i φ_{i,vedel} P \]

\[ y_i φ_{i,gaas} = x_i φ_{i,vedel} \]

Fugitiivsuse koefitsienti saab arvutada olekuvõrrandiga.

Aktiivsuse koefitsient

Minevikus polnud head olekuvõrrandit vedelfaasi jaoks. Sellepärast, töötati välja meetodit, mis kasutab hoopis aktiivsuse koefitsienti vedelfaasi fugitiivsuse arvutamiseks.

Aktiivsuse koefitsient on aine fugitiivsus segus jagatud puhta aine fugitiivsusega samadel tingimustel. Nimetajas puhta aine fugitiivsust korrutatakse ka aine moolosaga, nii et suurused oleksid võrreldavad.

\[ γ_i = \frac{f_i}{f_{i,puhas} x_i} \]

Aktiivsuse koefitsient näitab erinevust ideaalsest segunemisest. Ideaalne segu tähendab, et segu omadus saab arvutada, kui korrutada iga komponendi puhta aine omadust moolosaga segus ja siis need väärtused kokku liita.

\[ Θ_{ideaalne\ segu} = \sum_{i} Θ_{i,puhas} x_i \]

Teiste sõnadega, segu on ideaalne, kui tõmbejoud erinevate molekulide vahel segus on sarnased neile, mis esinevad aine oma molekulide vahel. Reaalses segus ained on tavaliselt piisavalt erinevad, et fugitiivsus muudab koostisega. Aktiivsuse koefitsient eraldab segunemise mõju.

Aktiivsus koefitsienti saab arvutada erinevate mudelitega.

Tasakaal aktiivsuse koefitsiendiga

Me saame nüüd asendada vedelfaasi fugitiivsuse koefitsiendi aktiivsuse koefitsiendiga. Seda meetodit kutsutakse mõnikord γ-φ meetodiks.

\[ y_i φ_{i,gaas} P = x_i γ_i φ^{sat}_{i,vedel} P^{sat}_i \exp \left( \int_{P_i^{sat}}^{P} \frac{V_i}{RT} dp \right) \]

Nagu näha, tasakaalu valem on nüüd keerulisem. Aktiivsuse koefitsient ei võta arvesse nii palju mõjusid, kui fugitiivsuse koefitsient. Sellepärast, on vaja lisada need teised osad valemis, mis võtavad need mõjud arvesse.

Näiteks, exponentsiaal valemi lõpul on Poyntingi parandustegur, mis võtab arvesse rõhu erinevuse mõju segu fugitiivsusele. On rõhu erinevus kuna aine aururõhk (P^sat) ei ole päris sama kui segu rõhk (P). Tavaliselt, rõhu mõju on ainult oluline, kui süsteemi rõhk on kõrge. Seega, madalamal rõhul saame tavaliselt valemit lihtsustada jättes Poyntingi parandusteguri välja.

\[ y_i φ_{i,gaas} P = x_i γ_i φ^{sat}_{i,vedel} P^{sat}_i \]

Valemis on samuti puhta aine vedelfaasi fugitiivsuse koefitsient aururõhul (\( φ^{sat}_{i,vedel} \)). See võtab arvesse aine kõrvalekallet ideaalsest käitumisest. Pea meeles, et aktiivsuse koefitsient võtab arvesse ainult kõrvalekallet, mis tuleb segunemisest. Isegi puhta ainega esinevad kõrvalekalded ideaalsest käitumisest ja \( φ^{sat}_{i,vedel} \) võtab need arvesse. Kui eeldame, et puhta aine vedelfaasi fugitiivsuse koefitsient on ühe lähedal, siis saame selle valemist välja jätta. See eeldus tavaliselt sobib, kui rõhk on madal.

\[ y_i φ_{i,gaas} P = x_i γ_i P^{sat}_i \]

Gaasifaasi jaoks ikkagi kasutatakse fugitiivsuse koefitsienti selleks, et arvutada kõrvalekallet ideaalsest käitumisest. Selle arvutamiseks saab kasutada ka lihtsamaid olekuvõrrandeid nagu kuupvõrrandeid. Kui eeldame, et gaasifaas käitub ideaalselt, siis saame valemit veelgi lihtsustada jättes välja gaasifaasi fugitiivsuse koefitsiendi.

\[ y_i P = x_i γ_i P^{sat}_i \]

Ja kui eeldame, et vedelfaas on ideaalne segu (ehk segunemine ei mõjuta fugitiivsust), siis võime aktiivsuse koefitsiendi kõrvale jätta ja jõuame tagasi Raoulti seaduseni.

Muud tasakaalud

Siiamaani oleme keskendanud auru-vedel tasakaalule, aga esinevad tasakaalud ka teiste faaside vahel.

Vedel-vedel tasakaal,
Tahke-vedel tasakaal,
Gaasi-tahke tasakaal,
Vedel-vedel-vedel tasakaal,
Tahke-vedel-vedel tasakaal,
Tahke-tahke tasakaal.

Selleks, et arvutada tasakaalu tingimusi muude tasakaalude jaoks on vaja lihtsalt valemit mõlema faasi fugitiivsuse jaoks. Näiteks, vedel-vedel tasakaalu jaoks võime kasutada samad valemid vedelfaasi jaoks, mida me oleme kasutanud auru-vedel tasakaalu arvutustes. Kui kasutada olekuvõrrandit (nt PC-SAFT), et otse arvutada fugitiivsuse koefitsienti, siis vedel-vedel tasakaalu valem on selline:

\[ x_{i,A} φ_{i,A} = x_{i,B} φ_{i,B} \]

Võime samuti arvutada vedel-vedel tasakaalu aktiivsuse koefitsiendiga:

\[ x_{i,A} γ_{i,A} φ^{sat}_{i,A} P^{sat}_{i,A} = x_{i,B} γ_{i,B} φ^{sat}_{i,B} P^{sat}_{i,B} \]

Ja kuna aururõhk ja \( φ^{sat}_{i} \) on mõlema faasi jaoks sama (on ju sama aine), need taanduvad välja.

\[ x_{i,A} γ_{i,A} = x_{i,B} γ_{i,B} \]

Viited

P. Uusi-Kyyny, J.-P. Pokki, J. Aittamaa, and S. Liukkonen, “Vapor−Liquid Equilibrium for the Binary Systems of 3-Methylpentane + 2-Methyl-2-propanol at 331 K and + 2-Butanol at 331 K,” Journal of Chemical & Engineering Data, vol. 46, no. 3, pp. 754–758, May 2001, doi: 10.1021/je000295w.
L. Albright, Albright’s Chemical Engineering Handbook. CRC Press, 2008.
J. P. O’Connell and J. M. Haile, Thermodynamics: Fundamentals for Applications. Cambridge University Press, 2005.
M. Uyan, G. Sieder, T. Ingram, and C. Held, “Predicting CO2 solubility in aqueous N-methyldiethanolamine solutions with ePC-SAFT,” Fluid Phase Equilibria, vol. 393, pp. 91–100, May 2015, doi:10.1016/j.fluid.2015.02.026.
M. D. Koretsky, Engineering and Chemical Thermodynamics. John Wiley & Sons, 2012.
Y. Thio, “Vapor Liquid Equilibrium: A Guide”. MIT Chemical Engineering Thermodynamics course. 2002. http://web.mit.edu/10.213/www/handouts/vle.pdf
R. Smith, Chemical Process Design and Integration. John Wiley & Sons, 2016.