Bioreaktorid

Elus organismide sees toimuvad paljud reaktsioonid. Reaktsiooniprotsesside põhimõtetega võime kirjeldada neid reaktsioone, mis toimuvad organismides ja võime isegi kasutada neid kemikaalide tootmiseks. Bioreaktoriga saame toota kemikaale, mida oleks raske toota ilma organismi abita.

Ensüümide kineetika

Ensüümid on suured bioloogilised molekulid, mis kiirendavad reaktsioone. Ensüümid on üldiselt valgud. Reaktsioonis ensüüm seob reagenti moodustades aktiivset siirdeseisundit, mida kutsutakse ensüüm-lähteaine kompleksiks (ingl enzyme-substrate complex). Ensüümide üks eelis on see, et need võivad väga selektiivselt toota just soovitud produkti kuna liituvad ainult teatud molekulidega ja viivad läbi tavaliselt ainult ühte reaktsiooni. Selle imelise katalüütilise võime saavutamiseks, ensüümid on kokku volditud nii, et neil oleks õige kuju ensüüm-lähteaine kompleksi moodustamiseks. Tagajärg on aga see, et ensüümid on tundlikud tingimustele reaktoris. Selleks, et nad töötaksid temperatuur peab olema tavaliselt 20 ja 70 °C vahel ja pH 4 ja 9 vahel. Kui temperatuur on liiga kõrge või pH on liiga äärmuslik, siis ensüümid võivad denatureerida, ehk nad kaotavad oma kuju ja enam ei saa reaktsioonis osaleda.

Kui kasutatakse sõna bioreaktor, siis tavaliselt peetakse silmas, et reaktoris on elus rakud ja, et ensüümi reaktsioonid toimuvad rakkudes. Kuid on võimalik ka eraldada ensüüme rakkudest ja mõnikord lisatakse ainult ensüüme reaktorisse.

Ensüümis on teatud aktiivsed kohad, mille juures reaktsioonid toimuvad. Need toimekohad seovad lähteainet ja panevad seda seisundisse, mis soodustab reaktsiooni. Üldist mehhanismi võib näidata järgnevalt:

\[ S + E \leftrightarrow E \cdot S \rightarrow P + E \]

Siin E on ensüüm, S on lähteaine ja P on produkt. Esimeses sammus ensüüm ja lähteaine liituvad moodustades ensüüm-lähteaine kompleksi. See samm on pöörduv ja lähteaine võib lahkude ensüümist enne, kui reaktsioon võib toimuda. Ensüüm-lähteaine kompleksist võib edasi toimuda reaktsiooni produkti moodustamiseks. Reaktsioonis võivad osaleda ka mitu lähteainet ja on võimalik, et reaktsioonis tekkivad mitu produkti.

Tahaksime ka arvutada reaktsiooni kiirust. Kasutatakse erinevaid valemeid ensüümi reaktsioonide kiiruse arvutamiseks, aga üks levinumaid on Michaelis-Menteni võrrand.

\[ -r_{S} = \frac{k_{cat} C_E C_S}{K_m + C_S} \]

Selles valemis S tähendab lähteaine (ingl substrate) ja C_E on ensüümi kontsentratsioon. k_cat näitab kui mitu lähteaine molekuli üks ensüümi molekul (ühe toimekohaga) suudab muundata teatud aja jooksul siis, kui toimekohas on alati lähteaine molekul (ehk lähteaine kontsentratsiooni ei piira reaktsiooni). Mõnikord kasutatakse hoopis V_max, mis näitab maksimaalset reaktsiooni kiirust, mida on võimalik saavutada konkreetse ensüümi kontsentratsiooni juures. Ehk, \( V_{max} = k_{cat} C_E \). K_m on Michaelis-Menteni konstant. K_m peaks ligikaudselt näitama, kui tugevasti ensüüm on seotud lähteainega. Iga reaktsioonil ja ensüümil on omad konstandi väärtused.

Vaatame natuke lähemalt Michaelis-Menteni võrrandi käitumist. Kui lähteaine kontsentratsioon on madal, siis nimetaja sisuliselt võrdub K_m-iga. Ehk, kiirus sõltub sisuliselt lineaarselt kontsentratsioonist ja reaktsioon käitub nagu esimest järku reaktsioon. Seda võib näha ka allolevast joonisest. Kui aga lähteaine kontsentratsioon on kõrge, nimetaja on ligikaudselt võrdne C_S-iga ja reaktsiooni kiirus eriti ei sõltu kontsentratsioonist. Ehk, näib, et reaktsiooni järk on null. See käitumine on loogiline kuna kõrge lähteaine kontsentratsiooni puhul peaaegu kõik ensüümi toimekohad on hõivatud ja lähteainet lisamine ei saa väga mõjutada reaktsiooni kiirust.

Tuleks ka mainida, et süsteemis võivad esineda muud ained, mis võivad takistada reaktsiooni. Neid kutsutakse aeglustiteks või inhibiitoriteks (ingl inhibitor). Need aeglustid on tavaliselt ained, mis liituvad ensüümiga ja ei võimalda lähteainel pääseda ensüümile ligi. Sel juhul kineetika on keerulisem ja reaktsiooni kiirus väheneb.

Rakkude kasv

Tavaliselt, bioreaktoris on elus rakud, mis oma elu tegevuse käigus toodavad mingit soovitud produkti. Rakud on küllaltki keerulised asjad, aga lihtsustades saame käsitleda rakkusid kui üks komponent ja saame koostada lihtsustatud reaktsiooni valemit.

\[ rakud + toitained \rightarrow rohkem rakud + produkt \]

Ühes süsteemis, näiteks bioreaktoris, organismid tavaliselt läbivad mitu erinevat kasvu faasi.

Viivitusfaas - organismid kohanevad uue keskkonnaga ja kasvu eriti ei toimu;
Eksponentsiaalne kasvufaas - organismid kasvavad ja paljunevad kiirest;
Statsionaarne faas - toidu-, ruumi- või mõne muu puudus piirab kasvu ja organismide kontsentratsioon püsib samal tasamel;
Surmafaas - toitu jääb väheks või mürgid tekivad elutegevuse tõttu ja organismid hakkavad surema.

Viivitusfaasi pikkus sõltub sellest, kui sarnane keskkond on organismide varasemale keskkonnale. Kui näiteks bakterid olid hoitud sarnastel tingimustel, siis bioreaktoris nad võibolla ei pea väga kohanema ja viivitusfaas ei pruugi juhtuda.

Produkt võib tekkida eksponentsiaalses kasvufaasis või statsionaarses faasis. Mõnikord organismid hakkavad soovitud ainet tootma alles siis, kui tekivad pinged. Näiteks, bioõli tootmisel mõned vetikad hakkavad tootma lipiide suuremates kogustes alles siis, kui tekib mingi pinge, mis neid häirib.⁹ Kui on teada, mis kasvufaasis produkt kõige rohkem tekib, siis saab paremini disainida bioreaktorit selleks, et suurendada saagist.

Rakkude kasvu saab kirjeldada ka kiiruse valemiga. Kasutatakse palju erinevaid valemeid, aga kõige rohkem kasutatakse Monodi võrrandit:

\[ r_{rakud} = \mu C_{rakud} \]

μ on rakkude erikasvukiirus. Monodi võrrandis seda arvutatakse järgmise valemiga.

\[ \mu = \mu_{max} \frac{C_S}{K_S + C_S} \]

Ehk, arvutatakse erikasvukiirust, kui osa maksimaalsest kasvukiirusest. Liites need kaks valemit saame sellise võrrandi:

\[ r_{rakud} = \frac{\mu_{max} C_S}{K_S + C_S} C_{rakud} \]

Võrrandi kuju on tegelikult tuttav ja meenutab Michaelis-Menteni võrrandit, mis on loogiline kuna rakkude kasv sõltub ensüümidest.

Bilansid

Nii nagu teiste reaktorite puhul, on võimalik koostada materjalbilansse bioreaktorite jaoks. Lisaks bilanssidele lähteainete jaoks, on võimalik ka koostada bilanssi rakkude jaoks.

Massiülekanne

Bioreaktoris võib olla ka oluline võtta arvesse massiülekanne. Näiteks, organismid sageli vajavad hapnikku või süsihappegaasi. Seda tihti lisatakse gaasina reaktorisse ja gaasi mullid läbivad lahuse. Need gaasid peavad siis liikuma mullist lahusesse ja siis rakkudesse.

Näide - maks

Kui alkoholi juuakse, siis keha reageerib ja proovib seda etanooli muundata selleks, et vähendada etanooli kontsentratsiooni kehas. Enamasti, etanooli muundamine toimub maksas. Etanool maos ja soolastikus imetakse verre, ja kui veri jõuab maksani ensüümid hakkavad seda muundama.

Etanooli muundatakse maksas järgnevate reaktsioonide kaudu:

\[ CH_3CH_2OH + NAD^+ \leftrightarrow CH_3CHO + NADH + H^+ \] \[ CH_3CHO + NAD^+ \rightarrow CH_3COOH + NADH + H^+ \]

Ensüümid kiirendavad neid reaktsioone. Esimeses reaktsioonis alkoholdehüdrogenaas muudab etanooli atsetaldehüüdiks ja teises reaktsioonis aldehüüddehüdrogenaase abil atsetaldehüüd muutub atsetaadiks.

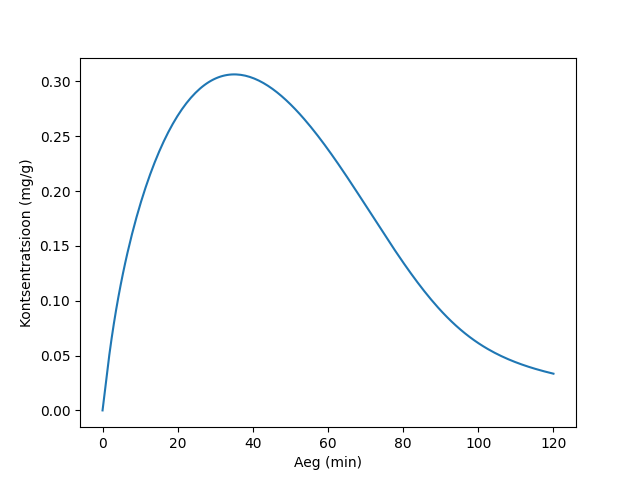
Tee mudelit sellest, kuidas etanooli kontsentratsioon muutub peale seda, kui juuakse alkohoolset jooki. Kui juuakse 120 ml veini (etanooli sisaldus 12 vol%), kas etanooli kontsentratsioon veres ületaks Eesti alkoholi piirmäära (0,2 promilli, ehk 0,2 mg/g)? Kui ületab, kui kaua läheks enne, kui etanooli kontsentratsioon veres on jälle madalam, kui piirmäär?

Mudeli lihtsustamiseks võib eeldata, et juuakse alkoholi kogust kõik korraga algushetkel. Võib ka teha keerulisemat mudelit, milles alkoholi juuakse mitu korda teatud aja jooksul.

Esiteks, koostame süsteemi skeemi. Kui alkohoolset jooki võetakse, siis esiteks läheb see makku. Maost mingil määral seda imetakse verre, kuid enamus liigub edasi soolestikku, kus imemine toimub palju kiiremini. Kui etanooli on imetud verre, siis see ringleb kehas ja läbib maksa. Kuigi reaktsioonid alkoholiga toimuvad mitmes kohas kehas, enamus etanooli muundatakse maksas.

Võime nüüd hakata koostama mudelit. Võtame järjest iga elundi ja koostame moolbilansi. Alustame verega kuna tahame lõpuks teada etanooli kontsentratsiooni veres.

\[ V_{veri} \frac{dC_{et,veri}}{dt} = \dot n_{maost} + \dot n_{sool} - \dot n_{maksa} + \dot n_{maksast} \]

Kuna veres reaktsioonid etanooliga eriti ei toimu, siis oluline on ainult need vood, mis toovad etanooli verre või viivad etanooli maksa. Võime ka lahti kirjutada neid moolkulusid selleks, et saame neid arvutada. Etanooli liikumine maost ja soolestikust verre on massiläbikande protsess. Kirjeldame siin seda lihtsalt läbikande valemiga, milles korrutame läbikandetegurit (h) kontsentratsiooni vahega.

\[ \dot n_{maost} = h_{maost} (C_{et,magu} - C_{et_veri}) \] \[ \dot n_{sool} = h_{sool} (C_{et,sool} - C_{et_veri}) \]

Võime arvutada moolkulu maksa ja vere vahel korrutades vere mahtkulu, mis läheb ja tuleb maksast, vastava etanooli kontsentratsiooniga.

\[ \dot n_{maksa} = \dot v_{maks-veri} C_{et,veri} \] \[ \dot n_{maksast} = \dot v_{maks-veri} C_{et,maks} \]

Kui asendada need moolbilansis, siis etanooli moolbilanss veres on selline:

\[ V_{veri} \frac{dC_{et,veri}}{dt} = h_{maost} (C_{et,magu} - C_{et_veri}) + h_{sool} (C_{et,sool} - C_{et_veri}) - \dot v_{maks-veri} C_{et,veri} + \dot v_{maks-veri} C_{et,maks} \]

Moolbilansid mao ja soolestiku jaoks võime me sarnaselt koostada. Siin v_magu-sool on mahtkulu, mis voolab maost soolestikku.

\[ V_{magu} \frac{dC_{et,magu}}{dt} = -\dot n_{maost} - \dot v_{magu-sool} C_{et,magu} \] \[ V_{sool} \frac{dC_{et,sool}}{dt} = -\dot n_{sool} + \dot v_{magu-sool} C_{et,magu} \]

Viimasena, saame koostada moolbilansi maksa jaoks. Erinevalt teistest elunditest, maksas peame ka arvesse võtma etanooli muundamisreaktsiooni.

\[ V_{maks} \frac{dC_{et,maks}}{dt} = \dot v_{maks-veri} C_{et,veri} - \dot v_{maks-veri} C_{et,maks} + r_{et} \]

Etanooli muundamisreaktsiooni kiirust ensüümi abil saab arvutada Michaelis-Menteni võrrandiga.²

\[ r_{et} = \frac{k_{cat} C_{et,maks}}{K_m + C_{et,maks}} \]

Nüüd mudel on koostatud ja võime kasutada Gekko paketti selleks, et lahendada mudelit. Esiteks, saame arvutada etanooli kogust, mida juuakse sisse.

V_jook = 400 # ml, joogi maht
mahtosa_etanool = 0.12
etanooli_tihedus = 0.78954976 # g/ml
m_etanool_sisse = V_jook * mahtosa_etanool * etanooli_tihedus

Seejärel, paneme kirja parameetreid, mis on mudelis vajalikud. Enamus parameetreid on võimalik leida kirjandusest.^2-8

m = GEKKO()
maksu_mass = 1.5 # kg
mm = 46.07 # etanooli molaar mass (g/mol)
vere_tihedus = 1.0506 # g/ml
maksu_tihedus = 1.051 # g/ml
kcat = m.Param(value=10) # min^-1
C_ensüüm = m.Param(value=2e-4) # mol/l
Km = m.Param(value=1.2/1000) # M
V_maks = m.Param(value=maksu_mass / maksu_tihedus) # l
V_veri = m.Param(value=5) # l
V_magu = m.Param(value=0.5 + V_jook/1000) # l, mao maht
V_sool = m.Param(value=0.06) # l, soolestiku maht
vdot_magu_sool = m.Param(value=0.01) # l/min, mahtkulu maost soolestikku
vdot_maks_veri = m.Param(value=maksu_mass) # l/min, vere mahtkulu maksasse on umbes 1 l / kg maksa.
h_magu = m.Param(value=0.0005) # min^-1
h_sool = m.Param(value=0.05) # min^-1
Cet_magu_alg = m_etanool_sisse / mm / V_magu.value # arvutada etanooli algkontsentratsioon kõhus

Peame ka valima ajahetki, mille juures sooviksime, et lahendust oleks arvutatud.

t_lõpp = 120 # min
npts = 200
m.time = np.linspace(0, t_lõpp, npts) # min

Lähteandmed on nüüd kirjas ja võime defineerida muutujaid, mida on vaja arvutada. Meie muutujad on etanooli kontsentratsioon neljas erinevas elundis.

Cet_magu = m.Var(Cet_magu_alg) # mol/l, etanooli kontsentratsioon maos
Cet_sool = m.Var(0) # mol/l, etanooli kontsentratsioon soolestikus
Cet_veri = m.Var(0) # mol/l, etanooli kontsentratsioon veres
Cet_maks = m.Var(0) # mol/l, etanooli kontsentratsioon maksas

Ja mudelit paneme kirja võrrandisüsteemina. Meil on neli moolbilansi, üks iga elundi jaoks. Kasutame ka Gekko Intermediate objekti selleks, et eraldi defineerida reaktsiooni kiirust ja moolkulu maost ja soolestikus verre. Seda tehes moolbilansid on natuke lihtsamad ja on võibolla kergem lugeda.

r = m.Intermediate(-kcat * C_ensüüm * Cet_maks / (Km + Cet_maks))
ndot_maost = m.Intermediate(h_magu * (Cet_magu - Cet_veri)) # mol/min
ndot_sool = m.Intermediate(h_sool * (Cet_sool - Cet_veri)) # mol/min
m.Equation(Cet_magu.dt() == (-ndot_maost - vdot_magu_sool * Cet_magu) / V_magu) # tegelikult mao maht pidevalt muutub, aga siin lihtsustame ja oletame, et maht ei muutu.
m.Equation(Cet_sool.dt() == (vdot_magu_sool * Cet_magu - ndot_sool) / V_sool)
m.Equation(Cet_veri.dt() == (ndot_maost + ndot_sool - vdot_maks_veri * Cet_veri + vdot_maks_veri * Cet_maks) / V_veri)
m.Equation(Cet_maks.dt() == (vdot_maks_veri * Cet_veri - vdot_maks_veri * Cet_maks + r * V_maks) / V_maks)

Nüüd saame lahendada mudelit. Teeme ka joonist nägemaks, kuidas etanooli kontsentratsioon veres muutub ajas. Teisendame kontsentratsiooni ühikut, nii et ühik oleks mg/g, ehk promiil.

m.options.IMODE = 4
m.solve(disp=False)

plt.figure()
plt.plot(m.time, np.asarray(Cet_veri.value) * mm / vere_tihedus)
plt.xlabel('Aeg (min)')
plt.ylabel('Kontsentratsioon (mg/g)')
plt.show()

Pythoni fail, mida kasutasime siin lahendamiseks, on võimalik kätte saada Githubist.

Viited

H. S. Fogler, Essentials of Chemical Reaction Engineering. Pearson Education, 2010.
F. W. Wagner, A. R. Burger, and B. L. Vallee, “Kinetic properties of human liver alcohol dehydrogenase: oxidation of alcohols by class I isoenzymes,” Biochemistry, vol. 22, no. 8, pp. 1857–1863, Apr. 1983, doi: 10.1021/bi00277a018.
C. Eipel, K. Abshagen, and B. Vollmar, “Regulation of hepatic blood flow: The hepatic arterial buffer response revisited,” World Journal of Gastroenterology : WJG, vol. 16, no. 48, p. 6046, Dec. 2010, doi: 10.3748/wjg.v16.i48.6046.
https://hypertextbook.com/facts/2004/MaryPennisi.shtml
R. J. Trudnowski and R. C. Rico, “Specific Gravity of Blood and Plasma at 4 and 37 °C,” Clinical Chemistry, vol. 20, no. 5, pp. 615–616, May 1974, doi: 10.1093/clinchem/20.5.615.
B. A. Overmoyer, C. E. McLaren, and G. M. Brittenham, “Uniformity of liver density and nonheme (storage) iron distribution,” Arch Pathol Lab Med, vol. 111, no. 6, pp. 549–554, Jun. 1987.
J. Feldschuh and Y. Enson, “Prediction of the normal blood volume. Relation of blood volume to body habitus.,” Circulation, vol. 56, no. 4, pp. 605–612, Oct. 1977, doi: 10.1161/01.CIR.56.4.605.
T. K. Li, W. F. Bosron, W. P. Dafeldecker, L. G. Lange, and B. L. Vallee, “Isolation of pi-alcohol dehydrogenase of human liver: is it a determinant of alcoholism?,” Proc Natl Acad Sci U S A, vol. 74, no. 10, pp. 4378–4381, Oct. 1977, doi: 10.1073/pnas.74.10.4378.
N. Pushpakumari Kudahettige, J. Pickova, and F. G. Gentili, “Stressing Algae for Biofuel Production: Biomass and Biochemical Composition of Scenedesmus dimorphus and Selenastrum minutum Grown in Municipal Untreated Wastewater,” Frontiers in Energy Research, vol. 6, p. 132, 2018, doi: 10.3389/fenrg.2018.00132.